@Article{AAM-36-4,
author = {Yan, Gaosheng and Lian, Hairong and Xinyu, Fang and Yue, Gao},
title = {Existence of Unbounded Solutions for a $n$-th Order BVPs with a $p$-Laplacian},
journal = {Annals of Applied Mathematics},
year = {2020},
volume = {36},
number = {4},
pages = {391--406},
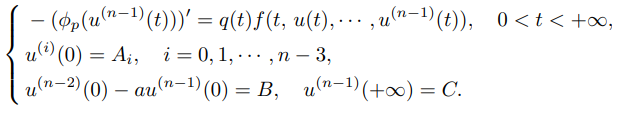
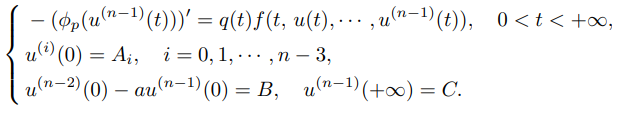
abstract = {<p style="text-align: justify;">This paper considers the solvability of boundary value problems with a $p$-Laplacian<br/></p><p style="text-align:center"><img src="https://admin.global-sci.org/uploads/ueditor/image/20210119/1611047173599195.png" title="1611047173599195.png" alt="image.png"/></p><p style="text-align: justify;">By using the methods of upper and lower solution, the schäuder fixed point
theorem, and the degree theory, we obtain the existence of one and triple
solutions. This paper generalizes several problems due to the dependence on
the $p$-Laplacian operator, the $n − 1$-th derivative not only in the differential
equation but also in the boundary conditions. The most interesting point is
that the solutions may be unbounded.</p>},
issn = {},
doi = {https://doi.org/2020-AAM-18587},
url = {https://global-sci.com/article/72672/existence-of-unbounded-solutions-for-a-n-th-order-bvps-with-a-p-laplacian}
}