@Article{AAM-35-3,
author = {Daomin, Cao and Zhongyuan, Liu},
title = {Multiple Vortices for the Shallow Water Equation in Two Dimensions},
journal = {Annals of Applied Mathematics},
year = {2019},
volume = {35},
number = {3},
pages = {221--249},
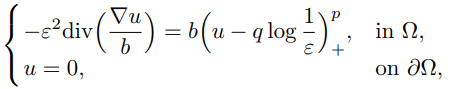
abstract = {<p style="text-align: justify;">In this paper, we construct stationary classical solutions of the shallow
water equation with vanishing Froude number $Fr$ in the so-called lake model.
To this end we need to study solutions to the following semilinear elliptic
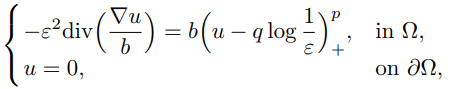
problem<br/></p><p style="text-align:center"><img src="http://admin.global-sci.org/uploads/ueditor/image/20200824/1598255508654041.png" title="1598255508654041.png" alt="image.png"/></p><p style="text-align: justify;">for small $ε$ &gt; 0, where $p$ &gt; 1, div($\frac{∇q}{b}$)
= 0 and $Ω$ ⊂ $\mathbb{R}$<sup>2&nbsp;</sup>is a smooth bounded
domain.<br/>We show that if <span style="text-align: justify;">$\frac{q^2}{b}$&nbsp;</span>has $m$ strictly local minimum (maximum) points $\widetilde{z}_i$, $i$ =
1, · · · , $m$, then there is a stationary classical solution approximating stationary $m$ points vortex solution of shallow water equations with vorticity $\sum\limits_{i=1}^m$ $\frac{2πq(\widetilde{z}_i)}{b(\widetilde{z}_i)}$.
Moreover, strictly local minimum points of <span style="text-align: justify;">$\frac{q^2}{b}$&nbsp;</span>on the boundary can also give
vortex solutions for the shallow water equation.</p>},
issn = {},
doi = {https://doi.org/2019-AAM-18081},
url = {https://global-sci.com/article/72683/multiple-vortices-for-the-shallow-water-equation-in-two-dimensions}
}