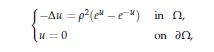
In this paper we consider the Dirichlet problem
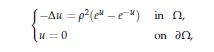
where $\rho$ is a small parameter and $\Omega$ is a $C^2$ bounded domain in $\mathbb{R}^2$. In [1], the author proves the existence of a $m$-point blow-up solution $u_\rho$ jointly with its asymptotic behaviour. We compute the Morse index of $u_\rho$ in terms of the Morse index of the associated Hamilton function of this problem. In addition, we give an asymptotic estimate for the first $4m$ eigenvalues and eigenfunctions.
}, issn = {1573-8175}, doi = {https://doi.org/10.4208/ata.OA-2020-0037}, url = {https://global-sci.com/article/73746/morse-index-of-multiple-blow-up-solutions-to-the-two-dimensional-sinh-poisson-equation} }