@Article{JCM-28-2,
author = {T., Hale, Elaine and Yin, Wotao and Zhang, Yin},
title = {Fixed-Point Continuation Applied to Compressed Sensing: Implementation and Numerical Experiments},
journal = {Journal of Computational Mathematics},
year = {2010},
volume = {28},
number = {2},
pages = {170--194},
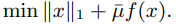
abstract = {<p style="text-align: justify;">Fixed-point continuation (FPC) is an approach, based on operator-splitting and continuation, for solving minimization problems with $\ell_1$-regularization:<br/> <br/></p><p style="text-align:center"><img src="https://admin.global-sci.org/uploads/ueditor/image/20210401/1617271753941055.png" title="1617271753941055.png" alt="image.png"/></p><p style="text-align: justify;"><br/>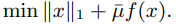We investigate the application of this algorithm to compressed sensing signal recovery, in which $f(x) = \frac{1}{2}\|Ax-b\|_M^2$, $A \in \mathbb{R}^{m \times n}$ and $m \leq n$. &nbsp;In particular, we extend the original algorithm to obtain better practical results, derive appropriate choices for $M$ and $\bar{\mu}$ under a given measurement model, and present numerical results for a variety of compressed sensing problems. The numerical results show that the performance of our algorithm compares favorably with that of several recently proposed algorithms.<br/></p>},
issn = {1991-7139},
doi = {https://doi.org/10.4208/jcm.2009.10-m1007},
url = {https://global-sci.com/article/84802/fixed-point-continuation-applied-to-compressed-sensing-implementation-and-numerical-experiments}
}