@Article{JCM-22-4,
author = {Zhao, Jingjun and Wanrong, Cao and Mingzhu, Liu},
title = {Asymptotic Stability of Runge-Kutta Methods for the Pantograph Equations},
journal = {Journal of Computational Mathematics},
year = {2004},
volume = {22},
number = {4},
pages = {523--534},
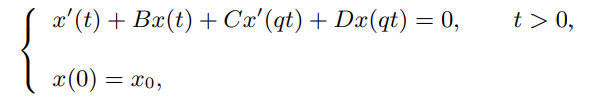
abstract = {<p style="text-align: justify;">This paper considers the asymptotic stability analysis of both exact and numerical solutions of the following neutral delay differential equation with pantograph delay.<br/></p><p style="text-align:center"><img src="https://admin.global-sci.org/uploads/ueditor/image/20210519/1621419035711473.png" title="1621419035711473.png" alt="image.png" width="405" height="67"/></p><p style="text-align: justify;">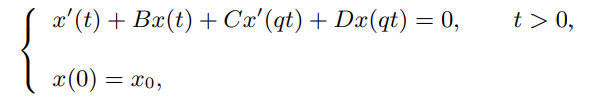where $B,C,D\in C^{d\times d},q\in (0,1)$,and $B$ is regular. After transforming the above equation to non-automatic neutral equation with constant delay, we determine sufficient conditions for the asymptotic stability of the zero solution. Furthermore, we focus on the asymptotic stability behavior of Runge-Kutta method with variable stepsize. It is proved that a L-stable Runge-Kutta method can preserve the above-mentioned stability properties. <br/></p>},
issn = {1991-7139},
doi = {https://doi.org/2004-JCM-8861},
url = {https://global-sci.com/article/85239/asymptotic-stability-of-runge-kutta-methods-for-the-pantograph-equations}
}