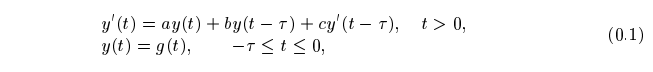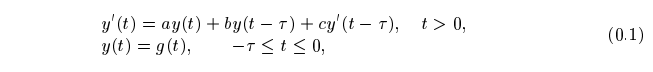@Article{JCM-20-2,
author = {Sory, Sidibe, Birama and Ming-Zhu, Liu},
title = {Asymptotic Stability for Gauss Methods for Neutral Delay Differential Equations},
journal = {Journal of Computational Mathematics},
year = {2002},
volume = {20},
number = {2},
pages = {217--224},
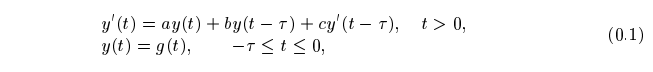
abstract = {<p style="text-align: justify;">In [4] we proved that all Gauss methods are $N \tau (0)$-compatible for neutral delay differential equations (NDDEs) of the form:<br/><img src="https://admin.global-sci.org/uploads/ueditor/image/20210803/1627962822498558.png" title="1627962822498558.png" alt="image.png"/><span style="text-align: center;"></span></p><p style="text-align: justify;">where $a, b, c$ are real, $\tau ＞0, g(t)$ is a continuous real valued function. In this paper we are going to use the theory of order stars to characterize the asymptotic stability properties of Gauss methods for NDDEs. And then proved that all Gauss methods are $N\tau(0)-$stable.<br/></p>},
issn = {1991-7139},
doi = {https://doi.org/2002-JCM-8912},
url = {https://global-sci.com/article/85401/asymptotic-stability-for-gauss-methods-for-neutral-delay-differential-equations}
}