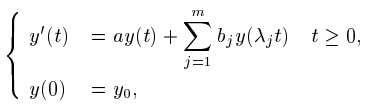
This paper deals with the asymptotic stability of theoretical solutions and numerical methods for the delay differential equations (DDEs)
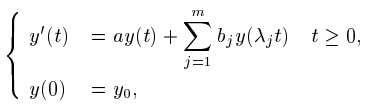
where $a, b_1, b_2, ... b_m$ and $y_0 \in C, 0 < \lambda_m \le \lambda_{m-1} \le ... \le \lambda_1<1$. A sufficient condition such that the differential equations are asymptotically stable is derived. And it is shown that the linear $\theta$-method is $\bigwedge GP_m$-stable if and only if $\frac{1}{2} \le \theta \le 1$.
}, issn = {1991-7139}, doi = {https://doi.org/1999-JCM-9122}, url = {https://global-sci.com/article/85648/the-numerical-stability-of-the-theta-method-for-delay-differential-equations-with-many-variable-delays} }