@Article{JNMA-3-1,
author = {Li, Fanfan and Zhenlai, Han},
title = {Oscillation Theory of $h$-Fractional Difference Equations},
journal = {Journal of Nonlinear Modeling and Analysis},
year = {2021},
volume = {3},
number = {1},
pages = {105--113},
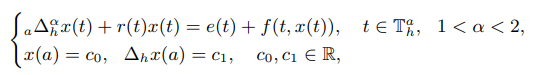
abstract = {<p style="text-align: justify;">In this paper, we initiate the oscillation theory for $h$-fractional
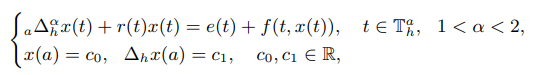
difference equations of the form<br/></p><p style="text-align:center"><img src="https://admin.global-sci.org/uploads/ueditor/image/20210506/1620268714544399.png" title="1620268714544399.png" alt="image.png"/></p><p style="text-align: justify;">where $_a∆^α_h$ is the Riemann-Liouville $h$-fractional difference of order $α$,&nbsp;$\mathbb{T}^a_h :$={$a + kh, k ∈&nbsp;\mathbb{Z}^+ $∪{0}}, and $a ≥ 0$, $h &gt; 0$. We study the oscillation of $h$-fractional difference equations with Riemann-Liouville derivative, and obtain
some sufficient conditions for oscillation of every solution. Finally, we give an
example to illustrate our main results.<br/></p>},
issn = {2562-2862},
doi = {https://doi.org/10.12150/jnma.2021.105},
url = {https://global-sci.com/article/87971/oscillation-theory-of-h-fractional-difference-equations}
}