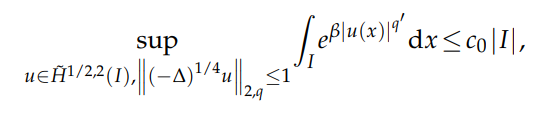
In this paper, we are concerned with a sharp fractional Trudinger-Moser type inequality in bounded intervals of R under the Lorentz-Sobolev norms constraint. For any $1<q<∞$ and $β≤ \big(\sqrt{π} \big)^{q'} \equiv β_q, q'= \frac{q}{q-1}$, we obtain
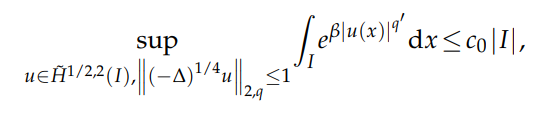
and $β_q$ is optimal in the sense that
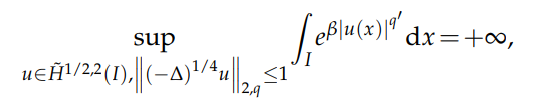
for any $β>β_q$. Furthermore, when $q$ is even, we obtain
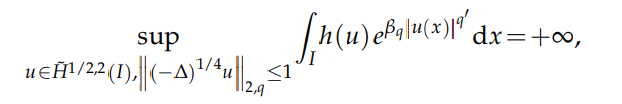
for any function $h : [0,∞)→[0,∞)$ with lim$_{t→∞} h(t) = ∞$. As for the key tools of proof, we use Green functions for fractional Laplace operators and the rearrangement of a convolution to the rearrangement of the convoluted functions.
}, issn = {2079-732X}, doi = {https://doi.org/10.4208/jpde.v34.n2.2}, url = {https://global-sci.com/article/88133/trudinger-moser-type-inequality-under-lorentz-sobolev-norms-constraint} }