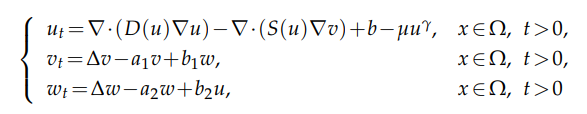
In this paper, we study the asymptotic behavior of solutions to a quasilinear
fully parabolic chemotaxis system with indirect signal production and logistic source
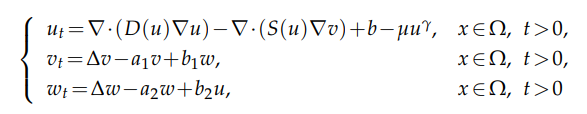
under homogeneous Neumann boundary conditions in a smooth bounded domain $Ω⊂\mathbb{R}^n$ $(n ≥1)$, where $b ≥0$, $γ ≥1$, $a_i ≥1$, $µ$, $b_i >0$ $(i =1,2)$, $D$, $S∈ C^2([0,∞))$ fulfilling $D(s) ≥ a_0(s+1)^{−α}$, $0 ≤ S(s) ≤ b_0(s+1)^β$ for all $s ≥ 0,$ where $a_0,b_0 > 0$ and $α,β ∈ \mathbb{R}$ are constants. The purpose of this paper is to prove that if $b ≥ 0$ and $µ > 0$ sufficiently large, the globally bounded solution $(u,v,w)$ with nonnegative initial data $(u_0,v_0,w_0)$ satisfies $$\Big\| u(·,t)− \Big(\frac{b}{µ}\Big)^{\frac{1}{γ}}\Big\|_{L^∞(Ω)}+\Big\| v(·,t)−\frac{b_1b_2}{a_1a_2} \Big(\frac{b}{µ}\Big)^{\frac{1}{γ}} \Big\| _{L^∞(Ω)} +\Big\| w(·,t)−\frac{b_2}{a_2}\Big(\frac{b}{µ}\Big)^{\frac{1}{γ}}\Big\| _{L^∞(Ω)} →0$$ as $t→∞$.
}, issn = {2079-732X}, doi = {https://doi.org/10.4208/jpde.v34.n2.3}, url = {https://global-sci.com/article/88134/asymptotic-behavior-in-a-quasilinear-fully-parabolic-chemotaxis-system-with-indirect-signal-production-and-logistic-source} }