The Nehari Manifold for a Class of Singular $\psi$-Riemann-Liouville Fractional with $p$-Laplacian Operator Differential Equations
Abstract
Using Nehari manifold method combined with fibring maps, we show the
existence of nontrivial, weak, positive solutions of the nonlinear $\psi$-Riemann-Liouville
fractional boundary value problem involving the $p$-Laplacian operator, given by
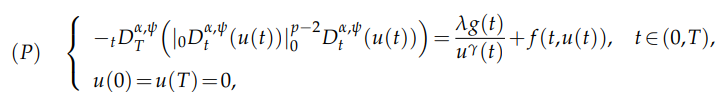
where $λ>0, 0<\gamma<1< p$ and $\frac{1}{p}<\alpha≤1,$ $g∈C([0,T])$ and $f ∈C^1
([0,T]×\mathbb{R},\mathbb{R}).$ A useful
examples are presented in order to illustrate the validity of our main results.
About this article








