Morse Index of Multiple Blow-up Solutions to the Two-Dimensional Sinh-Poisson Equation

Abstract

In this paper we consider the Dirichlet problem

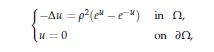
where $\rho$ is a small parameter and $\Omega$ is a $C^2$ bounded domain in $\mathbb{R}^2$. In [1], the author proves the existence of a $m$-point blow-up solution $u_\rho$ jointly with its asymptotic behaviour. We compute the Morse index of $u_\rho$ in terms of the Morse index of the associated Hamilton function of this problem. In addition, we give an asymptotic estimate for the first $4m$ eigenvalues and eigenfunctions.