Oscillation Theory of $h$-Fractional Difference Equations
Abstract
In this paper, we initiate the oscillation theory for $h$-fractional
difference equations of the form
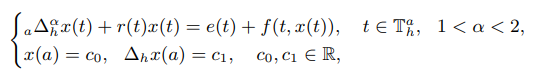
where $_a∆^α_h$ is the Riemann-Liouville $h$-fractional difference of order $α$, $\mathbb{T}^a_h :$={$a + kh, k ∈ \mathbb{Z}^+ $∪{0}}, and $a ≥ 0$, $h > 0$. We study the oscillation of $h$-fractional difference equations with Riemann-Liouville derivative, and obtain
some sufficient conditions for oscillation of every solution. Finally, we give an
example to illustrate our main results.
About this article
How to Cite
Oscillation Theory of $h$-Fractional Difference Equations. (2024). Journal of Nonlinear Modeling and Analysis, 3(1), 105-113. https://doi.org/10.12150/jnma.2021.105




