Study of Certain Navier Problems in Sobolev Space with Weights
Abstract
In this paper, we study the following Navier problem
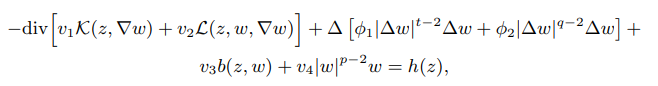
Here, $h ∈ L^{p'} (\mathcal{Q}, v^{1−p′}_1),$ $\mathcal{K}, \mathcal{L}$ and $b$ are Carathéodory functions and $ϕ_1,ϕ_2,$ $v_1,
v_2, v_3$ and $v_4$ are $A_p$-weights functions. By using the theory of monotone operators (Browder–Minty Theorem), we demonstrate the existence and uniqueness
of weak solution to the above problem.
About this article
How to Cite
Study of Certain Navier Problems in Sobolev Space with Weights. (2025). Journal of Nonlinear Modeling and Analysis, 7(4), 1332-1352. https://doi.org/10.12150/jnma.2025.1332




