CSIAM Trans. Appl. Math., 2 (2021), pp. 195-262.
Published online: 2021-05
Cited by
- BibTex
- RIS
- TXT
We consider the following constrained Rayleigh quotient optimization problem (CRQopt):
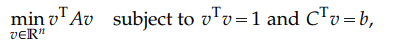
where $A$ is an $n×n$ real symmetric matrix and $C$ is an $n×m$ real matrix. Usually, $m$ « $n$. The problem is also known as the constrained eigenvalue problem in literature since it becomes an eigenvalue problem if the linear constraint $C$T$v=b$ is removed. We start by transforming CRQopt into an equivalent optimization problem (LGopt) of minimizing the Lagrangian multiplier of CRQopt, and then into another equivalent problem (QEPmin) of finding the smallest eigenvalue of a quadratic eigenvalue problem. Although these equivalences have been discussed in literature, it appears to be the first time that they are rigorously justified in this paper. In the second part, we present numerical algorithms for solving LGopt and QEPmin based on Krylov subspace projection. The basic idea is to first project LGopt and QEPmin onto Krylov subspaces to yield problems of the same types but of much smaller sizes, and then solve the reduced problems by direct methods, which is either a secular equation solver (in the case of LGopt) or an eigensolver (in the case of QEPmin). We provide convergence analysis for the proposed algorithms and present error bounds. The sharpness of the error bounds is demonstrated by examples, although in applications the algorithms often converge much faster than the bounds suggest. Finally, we apply the new algorithms to semi-supervised learning in the context of constrained clustering.
}, issn = {2708-0579}, doi = {https://doi.org/10.4208/csiam-am.2021.nla.01}, url = {http://global-sci.org/intro/article_detail/csiam-am/18884.html} }We consider the following constrained Rayleigh quotient optimization problem (CRQopt):
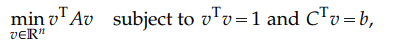
where $A$ is an $n×n$ real symmetric matrix and $C$ is an $n×m$ real matrix. Usually, $m$ « $n$. The problem is also known as the constrained eigenvalue problem in literature since it becomes an eigenvalue problem if the linear constraint $C$T$v=b$ is removed. We start by transforming CRQopt into an equivalent optimization problem (LGopt) of minimizing the Lagrangian multiplier of CRQopt, and then into another equivalent problem (QEPmin) of finding the smallest eigenvalue of a quadratic eigenvalue problem. Although these equivalences have been discussed in literature, it appears to be the first time that they are rigorously justified in this paper. In the second part, we present numerical algorithms for solving LGopt and QEPmin based on Krylov subspace projection. The basic idea is to first project LGopt and QEPmin onto Krylov subspaces to yield problems of the same types but of much smaller sizes, and then solve the reduced problems by direct methods, which is either a secular equation solver (in the case of LGopt) or an eigensolver (in the case of QEPmin). We provide convergence analysis for the proposed algorithms and present error bounds. The sharpness of the error bounds is demonstrated by examples, although in applications the algorithms often converge much faster than the bounds suggest. Finally, we apply the new algorithms to semi-supervised learning in the context of constrained clustering.
