Order Results for Algebraically Stable Mono-Implicit Runge-Kutta Methods
Abstract
It is well known that mono-implicit Runge-Kutta methods have been applied in the efficient numerical solution of initial or boundary value problems of ordinary differential equations. Burrage(1994) has shown that the order of an s-stage mono-implicit Runge-Kutta method is at most s+1 and the stage order is at most 3. In this paper, it is shown that the order of an s-stage mono-implicit Runge-Kutta method being algebraically stable is at most min $(\widetilde{s}, 4)$, and the stage order together with the optimal B-convergence order is at most min(s,2), where
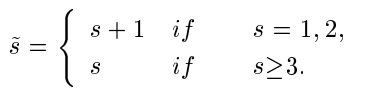
About this article
Abstract View
- 34332
Pdf View
- 3643
How to Cite
Order Results for Algebraically Stable Mono-Implicit Runge-Kutta Methods. (2021). Journal of Computational Mathematics, 17(6), 639-644. https://global-sci.com/index.php/JCM/article/view/11349




