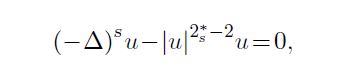In this paper, we consider the fractional  critical Schr\"odinger equation (FCSE)

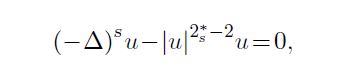
where $u \in \dot H^s( \mathbb{R}^N)$,  $N\geq 4$,  $0<s<1$  and $2^{\ast}_{s}=\frac{2N}{N-2s}$ is the critical Sobolev exponent of order $s$.

By virtue of the variational method and the concentration compactness principle with  the  equivariant group action, we obtain some new type of non-radial, sign-changing solutions of (FCSE) in the energy space $\dot H^s(\mathbb{R}^N)$. The key component is that we take the equivariant group action to construct several  subspace of $\dot H^s(\mathbb{R}^N)$  with trivial intersection, then combine the concentration compactness argument in the Sobolev space with fractional order  to show the compactness property of Palais-Smale sequences in each subspace and obtain the multiple solutions of (FCSE) in $\dot H^s(\mathbb{R}^N)$.