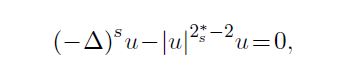In this paper, we consider the fractional critical Schr\"odinger equation (FCSE)
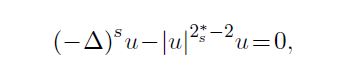
where $u \in \dot H^s( \mathbb{R}^N)$, $N\geq 4$, $0<s<1$ and $2^{\ast}_{s}=\frac{2N}{N-2s}$ is the critical Sobolev exponent of order $s$.
By virtue of the variational method and the concentration compactness principle with the equivariant group action, we obtain some new type of non-radial, sign-changing solutions of (FCSE) in the energy space $\dot H^s(\mathbb{R}^N)$. The key component is that we take the equivariant group action to construct several subspace of $\dot H^s(\mathbb{R}^N)$ with trivial intersection, then combine the concentration compactness argument in the Sobolev space with fractional order to show the compactness property of Palais-Smale sequences in each subspace and obtain the multiple solutions of (FCSE) in $\dot H^s(\mathbb{R}^N)$.