Multiple Positive Solutions for a Class of Integral Boundary Value Problem
Year: 2019
Author: Yang Yang, Yunrui Yang, Kepan Liu
Annals of Applied Mathematics, Vol. 35 (2019), Iss. 4 : pp. 364–373
Abstract
In this paper, the existence and multiplicity of positive solutions for a class
of non-resonant fourth-order integral boundary value problem
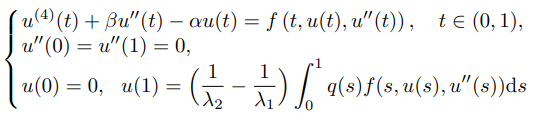
with two parameters are established by using the Guo-Krasnoselskii's fixed-point theorem, where f∈C([0,1]×[0,+∞)×(−∞,0], [0,+∞)), q(t)∈L1[0,1] is nonnegative, α,β∈R and satisfy β<2π2, α>0, α/π4+β/π2<1, λ1,2=(−β∓√β2+4α)/2. The corresponding examples are raised to demonstrate the results we obtained.
You do not have full access to this article.
Already a Subscriber? Sign in as an individual or via your institution
Journal Article Details
Publisher Name: Global Science Press
Language: English
DOI: https://doi.org/2019-AAM-18087
Annals of Applied Mathematics, Vol. 35 (2019), Iss. 4 : pp. 364–373
Published online: 2019-01
AMS Subject Headings: Global Science Press
Copyright: COPYRIGHT: © Global Science Press
Pages: 10
Keywords: positive solutions fixed point integral boundary conditions.
Author Details
Yang Yang Email
Yunrui Yang Email
Kepan Liu Email

