The Oseen Type Finite Element Iterative Method for the Stationary Incompressible Magnetohydrodynamics
Year: 2017
Author: Xiaojing Dong, Yinnian He
Advances in Applied Mathematics and Mechanics, Vol. 9 (2017), Iss. 4 : pp. 775–794
Abstract
In this article, by applying the Stokes projection and an orthogonal projection
with respect to curl and div operators, some new error estimates of finite element
method (FEM) for the stationary incompressible magnetohydrodynamics (MHD) are
obtained. To our knowledge, it is the first time to establish the error bounds which are
explicitly dependent on the Reynolds numbers, coupling number and mesh size. On
the other hand, The uniform stability and convergence of an Oseen type finite element
iterative method for MHD with respect to high hydrodynamic Reynolds number $R_e$ and magnetic Reynolds number $R_m$, or small $δ=1−σ$ with
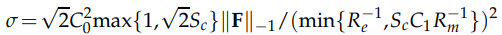
($C_0$, $C_1$ are constants depending only on $Ω$ and F is related to the source terms of equations) are analyzed under the condition that $h$≤(‖F‖$_{−1}$/‖F‖$_0$)$^{1/2}δ$. Finally, some numerical tests are presented to demonstrate the effectiveness of this algorithm.
You do not have full access to this article.
Already a Subscriber? Sign in as an individual or via your institution
Journal Article Details
Publisher Name: Global Science Press
Language: English
DOI: https://doi.org/10.4208/aamm.2015.m934
Advances in Applied Mathematics and Mechanics, Vol. 9 (2017), Iss. 4 : pp. 775–794
Published online: 2017-01
AMS Subject Headings: Global Science Press
Copyright: COPYRIGHT: © Global Science Press
Pages: 20
Keywords: Uniform stability convergence Oseen type iterative method finite element method stationary incompressible magnetohydrodynamics.
Author Details
-
The Arrow–Hurwicz iterative finite element method for the stationary magnetohydrodynamics flow
Yang, Yun-Bo | Jiang, Yao-Lin | Kong, Qiong-XiangApplied Mathematics and Computation, Vol. 356 (2019), Iss. P.347
https://doi.org/10.1016/j.amc.2018.10.050 [Citations: 3] -
Uniform Stability and Convergence with Respect to $$(\nu , \mu , s, 1-\sigma )$$ of the Three Iterative Finite Element Solutions for the 3D Steady MHD Equations
He, Yinnian | Dong, Xiaojing | Feng, XinlongJournal of Scientific Computing, Vol. 90 (2022), Iss. 1
https://doi.org/10.1007/s10915-021-01671-0 [Citations: 8] -
Optimal convergence analysis of Crank–Nicolson extrapolation scheme for the three-dimensional incompressible magnetohydrodynamics
Dong, Xiaojing | He, YinnianComputers & Mathematics with Applications, Vol. 76 (2018), Iss. 11-12 P.2678
https://doi.org/10.1016/j.camwa.2018.08.060 [Citations: 20] -
Uniform stability and convergence of the iterative solutions of the 3D steady viscous primitive equations of the ocean under the small depth assumption
He, Yinnian
Journal of Differential Equations, Vol. 335 (2022), Iss. P.549
https://doi.org/10.1016/j.jde.2022.07.011 [Citations: 0] -
A least squares finite element method using Elsasser variables for magnetohydrodynamic equations
Lee, Eunjung | Ha, Heonkyu | Kim, Sang DongJournal of Computational and Applied Mathematics, Vol. 346 (2019), Iss. P.599
https://doi.org/10.1016/j.cam.2018.06.038 [Citations: 0] -
Mixed Generalized Multiscale Finite Element Method for a Simplified Magnetohydrodynamics Problem in Perforated Domains
Alekseev, Valentin | Tang, Qili | Vasilyeva, Maria | Chung, Eric T. | Efendiev, YalchinComputation, Vol. 8 (2020), Iss. 2 P.58
https://doi.org/10.3390/computation8020058 [Citations: 3] -
Two-Level Finite Element Iterative Algorithm Based on Stabilized Method for the Stationary Incompressible Magnetohydrodynamics
Tang, Qili | Hou, Min | Xiao, Yajie | Yin, LinaEntropy, Vol. 24 (2022), Iss. 10 P.1426
https://doi.org/10.3390/e24101426 [Citations: 1]

