Year: 2020
Author: Yeon Hyang Kim, Roza Aceska
East Asian Journal on Applied Mathematics, Vol. 10 (2020), Iss. 4 : pp. 838–850
Abstract
Let $\{ƒ_n\}^∞_{n=1}$ be a basis for $L_2([0, 1])$ and $\{g_n\}^∞_{n=1}$ be a system of functions of controlled decay on [0,∞). Considering a function u(x, t) that can be the represented in the form
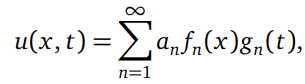
where an ∈ R, x ∈ [0, 1] and t ∈ [0,∞), we investigate whether the function ƒ(x) =
u(x, 0) can be approximated, in a reasonable sense, by using data u(x0, t1), u(x0, t2),...,
u(x0, tN). A mathematical framework and efficient computational schemes are developed to determine approximate solutions for various classes of partial differential equations via sampled data by first establishing a near-best approximation of ƒ .
You do not have full access to this article.
Already a Subscriber? Sign in as an individual or via your institution
Journal Article Details
Publisher Name: Global Science Press
Language: English
DOI: https://doi.org/10.4208/eajam.210220.120620
East Asian Journal on Applied Mathematics, Vol. 10 (2020), Iss. 4 : pp. 838–850
Published online: 2020-01
AMS Subject Headings:
Copyright: COPYRIGHT: © Global Science Press
Pages: 13
Keywords: Dynamical system evolutionary systems representation near-best approximation initial data PDEs.

