Year: 2004
Author: Jingjun Zhao, Wanrong Cao, Mingzhu Liu
Journal of Computational Mathematics, Vol. 22 (2004), Iss. 4 : pp. 523–534
Abstract
This paper considers the asymptotic stability analysis of both exact and numerical solutions of the following neutral delay differential equation with pantograph delay.
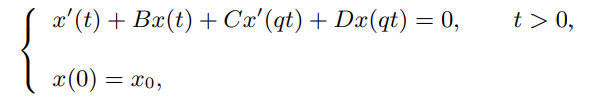
where $B,C,D\in C^{d\times d},q\in (0,1)$,and $B$ is regular. After transforming the above equation to non-automatic neutral equation with constant delay, we determine sufficient conditions for the asymptotic stability of the zero solution. Furthermore, we focus on the asymptotic stability behavior of Runge-Kutta method with variable stepsize. It is proved that a L-stable Runge-Kutta method can preserve the above-mentioned stability properties.
You do not have full access to this article.
Already a Subscriber? Sign in as an individual or via your institution
Journal Article Details
Publisher Name: Global Science Press
Language: English
DOI: https://doi.org/2004-JCM-8861
Journal of Computational Mathematics, Vol. 22 (2004), Iss. 4 : pp. 523–534
Published online: 2004-01
AMS Subject Headings:
Copyright: COPYRIGHT: © Global Science Press
Pages: 12
Keywords: Neutral delay differential equations Pantograph delay Asymptotic stability Runge-Kutta methods L-stable.

