Year: 2002
Author: Birama Sory Sidibe, Ming-Zhu Liu
Journal of Computational Mathematics, Vol. 20 (2002), Iss. 2 : pp. 217–224
Abstract
In [4] we proved that all Gauss methods are $N \tau (0)$-compatible for neutral delay differential equations (NDDEs) of the form: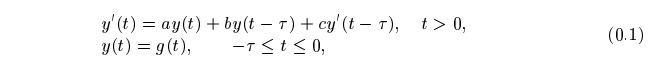
where $a, b, c$ are real, $\tau >0, g(t)$ is a continuous real valued function. In this paper we are going to use the theory of order stars to characterize the asymptotic stability properties of Gauss methods for NDDEs. And then proved that all Gauss methods are $N\tau(0)-$stable.
You do not have full access to this article.
Already a Subscriber? Sign in as an individual or via your institution
Journal Article Details
Publisher Name: Global Science Press
Language: English
DOI: https://doi.org/2002-JCM-8912
Journal of Computational Mathematics, Vol. 20 (2002), Iss. 2 : pp. 217–224
Published online: 2002-01
AMS Subject Headings:
Copyright: COPYRIGHT: © Global Science Press
Pages: 8
Keywords: Delay differential equations Stability Runge-Kutta methods.

