Year: 2001
Author: Yao-Tang Li, Ji-Cheng Li
Journal of Computational Mathematics, Vol. 19 (2001), Iss. 4 : pp. 365–370
Abstract
In this paper, some estimations of bounds for determinant of Hadamard product of H-matrices are given. The main result is the following if A=(aij) and B=(bij) are nonsingular H-matrices of order n and ∏ni=1aiibii>0, and Ak and Bk,k=1,2,⋯,n, are the k×k leading principal submatrices of A and B, respectively, then
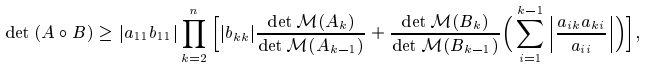
where M(Ak) denotes the comparison matrix of Ak.
You do not have full access to this article.
Already a Subscriber? Sign in as an individual or via your institution
Journal Article Details
Publisher Name: Global Science Press
Language: English
DOI: https://doi.org/2001-JCM-8989
Journal of Computational Mathematics, Vol. 19 (2001), Iss. 4 : pp. 365–370
Published online: 2001-01
AMS Subject Headings:
Copyright: COPYRIGHT: © Global Science Press
Pages: 6
Keywords: H-matrix Determinant Hadamard product.

