Year: 1999
Author: Ai-Guo Xiao
Journal of Computational Mathematics, Vol. 17 (1999), Iss. 6 : pp. 639–644
Abstract
It is well known that mono-implicit Runge-Kutta methods have been applied in the efficient numerical solution of initial or boundary value problems of ordinary differential equations. Burrage(1994) has shown that the order of an s-stage mono-implicit Runge-Kutta method is at most s+1 and the stage order is at most 3. In this paper, it is shown that the order of an s-stage mono-implicit Runge-Kutta method being algebraically stable is at most min $(\widetilde{s}, 4)$, and the stage order together with the optimal B-convergence order is at most min(s,2), where
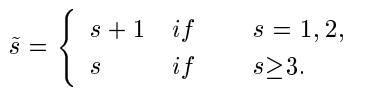
You do not have full access to this article.
Already a Subscriber? Sign in as an individual or via your institution
Journal Article Details
Publisher Name: Global Science Press
Language: English
DOI: https://doi.org/1999-JCM-9134
Journal of Computational Mathematics, Vol. 17 (1999), Iss. 6 : pp. 639–644
Published online: 1999-01
AMS Subject Headings:
Copyright: COPYRIGHT: © Global Science Press
Pages: 6

