Asymptotic Behavior in a Quasilinear Fully Parabolic Chemotaxis System with Indirect Signal Production and Logistic Source
Year: 2021
Author: Dan Li, Zhongping Li
Journal of Partial Differential Equations, Vol. 34 (2021), Iss. 2 : pp. 129–143
Abstract
In this paper, we study the asymptotic behavior of solutions to a quasilinear
fully parabolic chemotaxis system with indirect signal production and logistic source
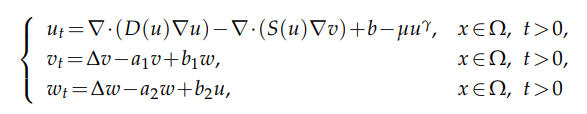
under homogeneous Neumann boundary conditions in a smooth bounded domain $Ω⊂\mathbb{R}^n$ $(n ≥1)$, where $b ≥0$, $γ ≥1$, $a_i ≥1$, $µ$, $b_i >0$ $(i =1,2)$, $D$, $S∈ C^2([0,∞))$ fulfilling $D(s) ≥ a_0(s+1)^{−α}$, $0 ≤ S(s) ≤ b_0(s+1)^β$ for all $s ≥ 0,$ where $a_0,b_0 > 0$ and $α,β ∈ \mathbb{R}$ are constants. The purpose of this paper is to prove that if $b ≥ 0$ and $µ > 0$ sufficiently large, the globally bounded solution $(u,v,w)$ with nonnegative initial data $(u_0,v_0,w_0)$ satisfies $$\Big\| u(·,t)− \Big(\frac{b}{µ}\Big)^{\frac{1}{γ}}\Big\|_{L^∞(Ω)}+\Big\| v(·,t)−\frac{b_1b_2}{a_1a_2} \Big(\frac{b}{µ}\Big)^{\frac{1}{γ}} \Big\| _{L^∞(Ω)} +\Big\| w(·,t)−\frac{b_2}{a_2}\Big(\frac{b}{µ}\Big)^{\frac{1}{γ}}\Big\| _{L^∞(Ω)} →0$$ as $t→∞$.
You do not have full access to this article.
Already a Subscriber? Sign in as an individual or via your institution
Journal Article Details
Publisher Name: Global Science Press
Language: English
DOI: https://doi.org/10.4208/jpde.v34.n2.3
Journal of Partial Differential Equations, Vol. 34 (2021), Iss. 2 : pp. 129–143
Published online: 2021-01
AMS Subject Headings:
Copyright: COPYRIGHT: © Global Science Press
Pages: 15
Keywords: Chemotaxis system indirect signal logistic source asymptotic behavior.

