Year: 2021
Author: 李佳傲
数学文化, Vol. 12 (2021), Iss. 4 : pp. 67–73
Abstract
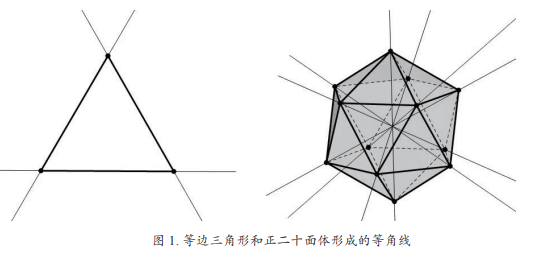
小时候，我们大概都会喜欢在纸上乱涂乱画。也许你想过这样一个问题 ：在纸上画一些直线，希望任意两条直线形成的夹角都相同，那么我们最多能画多少条这样的直线呢？对于纸面这样的二维平面，不难得到最多的数目是3条，等边三角形的3条边所构成的直线就是满足条件的构造。我们称这样的两两夹角相同的直线为等角线。那如果我们在三维欧式空间中寻找两两夹角相同的直线，最多能够有多少条呢？一个比较直观的想法是，三维坐标中3个坐标轴构成的直线两两垂直，这给出了3条等角线，但这不是最多的构造。在三维空间中，考虑一个正二十面体，它由20个面和12个顶点构成。通过连接相对顶点可以形成6条相交的对角线（如图1所示），可以看出其中任何一对直线都会形成一个固定的角。事实上，可以证明这个构造是最优的，即三维空间的等角线数目最多为6条，详见下文。
You do not have full access to this article.
Already a Subscriber? Sign in as an individual or via your institution
Journal Article Details
Publisher Name: Global Science Press
Language: Chinese
DOI: https://doi.org/2021-MC-19998
数学文化, Vol. 12 (2021), Iss. 4 : pp. 67–73
Published online: 2021-01
AMS Subject Headings:
Copyright: COPYRIGHT: © Global Science Press
Pages: 7