The Gradient Superconvergence of Bilinear Finite Volume Element for Elliptic Problems
Year: 2016
Numerical Mathematics: Theory, Methods and Applications, Vol. 9 (2016), Iss. 4 : pp. 579–594
Abstract
We study the gradient superconvergence of bilinear finite volume
element (FVE) solving the elliptic problems. First, a superclose
weak estimate is established for the bilinear form of the FVE
method. Then, we prove that the gradient approximation of the FVE
solution has the superconvergence property:
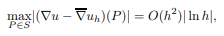
where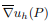 
denotes the average gradient on elements
containing point P and S is the set of optimal stress points
composed of the mesh points, the midpoints of edges and the centers of elements.
You do not have full access to this article.
Already a Subscriber? Sign in as an individual or via your institution
Journal Article Details
Publisher Name: Global Science Press
Language: English
DOI: https://doi.org/10.4208/nmtma.2016.m1515
Numerical Mathematics: Theory, Methods and Applications, Vol. 9 (2016), Iss. 4 : pp. 579–594
Published online: 2016-01
AMS Subject Headings:
Copyright: COPYRIGHT: © Global Science Press
Pages: 16