The Nehari Manifold for a Class of Singular $\psi$-Riemann-Liouville Fractional with $p$-Laplacian Operator Differential Equations
Year: 2024
Author: Samah Horrigue, Mona Alsulami, Bayan Abduallah Alsaeedi
Advances in Applied Mathematics and Mechanics, Vol. 16 (2024), Iss. 5 : pp. 1104–1120
Abstract
Using Nehari manifold method combined with fibring maps, we show the
existence of nontrivial, weak, positive solutions of the nonlinear $\psi$-Riemann-Liouville
fractional boundary value problem involving the $p$-Laplacian operator, given by
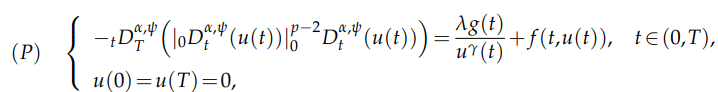
where $λ>0, 0<\gamma<1< p$ and $\frac{1}{p}<\alpha≤1,$ $g∈C([0,T])$ and $f ∈C^1
([0,T]×\mathbb{R},\mathbb{R}).$ A useful
examples are presented in order to illustrate the validity of our main results.
You do not have full access to this article.
Already a Subscriber? Sign in as an individual or via your institution
Journal Article Details
Publisher Name: Global Science Press
Language: English
DOI: https://doi.org/10.4208/aamm.OA-2022-0009
Advances in Applied Mathematics and Mechanics, Vol. 16 (2024), Iss. 5 : pp. 1104–1120
Published online: 2024-01
AMS Subject Headings: Global Science Press
Copyright: COPYRIGHT: © Global Science Press
Pages: 17
Keywords: $\psi$-Riemann-Liouville fractional derivative nonlinear fractional differential equations $p$-Laplacian operator existence of solutions Nehari manifold method.

