Convergence of an Embedded Exponential-Type Low-Regularity Integrators for the KdV Equation Without Loss of Regularity
Year: 2021
Author: Yongsheng Li, Yifei Wu, Fangyan Yao
Annals of Applied Mathematics, Vol. 37 (2021), Iss. 1 : pp. 1–21
Abstract
In this paper, we study the convergence rate of an Embedded exponential-type low-regularity integrator (ELRI) for the Korteweg-de Vries equation. We develop some new harmonic analysis techniques to handle the "stability" issue. In particular, we use a new stability estimate which allows us to avoid the use of the fractional Leibniz inequality,
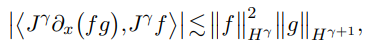
and replace it by suitable inequalities without loss of regularity. Based on these techniques, we prove that the ELRI scheme proposed in [41] provides 12-order convergence accuracy in Hγ for any initial data belonging to Hγ with γ>32, which does not require any additional derivative assumptions.
You do not have full access to this article.
Already a Subscriber? Sign in as an individual or via your institution
Journal Article Details
Publisher Name: Global Science Press
Language: English
DOI: https://doi.org/10.4208/aam.OA-2020-0001
Annals of Applied Mathematics, Vol. 37 (2021), Iss. 1 : pp. 1–21
Published online: 2021-01
AMS Subject Headings: Global Science Press
Copyright: COPYRIGHT: © Global Science Press
Pages: 21
Keywords: The KdV equation numerical solution convergence analysis error estimate low regularity fast Fourier transform.
Author Details
-
Quantifying and eliminating the time delay in stabilization exponential time differencing Runge–Kutta schemes for the Allen–Cahn equation
Zhang, Hong | Liu, Lele | Qian, Xu | Song, SongheESAIM: Mathematical Modelling and Numerical Analysis, Vol. 58 (2024), Iss. 1 P.191
https://doi.org/10.1051/m2an/2023101 [Citations: 2] -
Embedded exponential-type low-regularity integrators for KdV equation under rough data
Wu, Yifei | Zhao, XiaofeiBIT Numerical Mathematics, Vol. 62 (2022), Iss. 3 P.1049
https://doi.org/10.1007/s10543-021-00895-8 [Citations: 14] -
Low regularity exponential-type integrators for the “good” Boussinesq equation
Li, Hang | Su, ChunmeiIMA Journal of Numerical Analysis, Vol. 43 (2023), Iss. 6 P.3656
https://doi.org/10.1093/imanum/drac081 [Citations: 2] -
Time splitting method for nonlinear Schrödinger equation with rough initial data in L2
Choi, Hyung Jun | Kim, Seonghak | Koh, YoungwooJournal of Differential Equations, Vol. 417 (2025), Iss. P.164
https://doi.org/10.1016/j.jde.2024.11.018 [Citations: 0] -
A second-order low-regularity correction of Lie splitting for the semilinear Klein–Gordon equation
Li, Buyang | Schratz, Katharina | Zivcovich, FrancoESAIM: Mathematical Modelling and Numerical Analysis, Vol. 57 (2023), Iss. 2 P.899
https://doi.org/10.1051/m2an/2022096 [Citations: 1] -
A constructive low-regularity integrator for the one-dimensional cubic nonlinear Schrödinger equation under Neumann boundary condition
Bai, Genming | Li, Buyang | Wu, YifeiIMA Journal of Numerical Analysis, Vol. 43 (2023), Iss. 6 P.3243
https://doi.org/10.1093/imanum/drac075 [Citations: 3] -
An Embedded Exponential-Type Low-Regularity Integrator for mKdV Equation
Ning, Cui | Wu, Yifei | Zhao, XiaofeiSIAM Journal on Numerical Analysis, Vol. 60 (2022), Iss. 3 P.999
https://doi.org/10.1137/21M1408166 [Citations: 8] -
Gauge-Transformed Exponential Integrator for Generalized KdV Equations with Rough Data
Li, Bing | Wu, Yifei | Zhao, XiaofeiSIAM Journal on Numerical Analysis, Vol. 61 (2023), Iss. 4 P.1689
https://doi.org/10.1137/22M1530501 [Citations: 2] -
The BDF3/EP3 Scheme for MBE with No Slope Selection is Stable
Li, Dong | Quan, Chaoyu | Yang, WenJournal of Scientific Computing, Vol. 89 (2021), Iss. 2
https://doi.org/10.1007/s10915-021-01642-5 [Citations: 4] -
The Operator-Splitting Method for Cahn-Hilliard is Stable
Li, Dong | Quan, ChaoyuJournal of Scientific Computing, Vol. 90 (2022), Iss. 1
https://doi.org/10.1007/s10915-021-01740-4 [Citations: 8] -
A first-order Fourier integrator for the nonlinear Schrödinger equation on 𝕋 without loss of regularity
Wu, Yifei | Yao, FangyanMathematics of Computation, Vol. (2021), Iss.
https://doi.org/10.1090/mcom/3705 [Citations: 6]

