Year: 2020
Author: Gaosheng Yan, Hairong Lian, Xinyu Fang, Yue Gao
Annals of Applied Mathematics, Vol. 36 (2020), Iss. 4 : pp. 391–406
Abstract
This paper considers the solvability of boundary value problems with a $p$-Laplacian
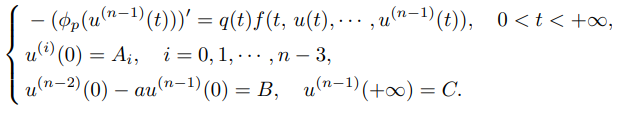
By using the methods of upper and lower solution, the schäuder fixed point theorem, and the degree theory, we obtain the existence of one and triple solutions. This paper generalizes several problems due to the dependence on the $p$-Laplacian operator, the $n − 1$-th derivative not only in the differential equation but also in the boundary conditions. The most interesting point is that the solutions may be unbounded.
You do not have full access to this article.
Already a Subscriber? Sign in as an individual or via your institution
Journal Article Details
Publisher Name: Global Science Press
Language: English
DOI: https://doi.org/2020-AAM-18587
Annals of Applied Mathematics, Vol. 36 (2020), Iss. 4 : pp. 391–406
Published online: 2020-01
AMS Subject Headings: Global Science Press
Copyright: COPYRIGHT: © Global Science Press
Pages: 16
Keywords: $p$-Laplacian upper solutions lower solutions infinite interval degree theory.

