Classification of Positive Ground State Solutions with Different Morse Indices for Nonlinear $N$-Coupled Schrödinger System
Year: 2021
Author: Juncheng Wei, Maoding Zhen
Analysis in Theory and Applications, Vol. 37 (2021), Iss. 2 : pp. 230–266
Abstract
In this paper, we study the following $N$-coupled nonlinear Schrödinger system
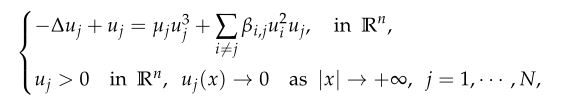
where $n\leq3,$ $ N\geq3$, $\mu_{j}>0, $ $\beta_{i, j}=\beta_{j, i}>0$ are constants and $\beta_{j, j}=\mu_{j},$ $ j=1, \cdots, N.$ There have been intensive studies for the system on existence/non-existence and classification of ground state solutions when $N=2$. However, fewer results about the classification of ground state solution are available for $N\geq3$. In this paper, we first give a complete classification result on ground state solutions with Morse indices $1,$ $2$ or $3$ for three-coupled Schrödinger system. Then we generalize our results to $N$-coupled Schrödinger system for ground state solutions with Morse indices 1 and $N$. We show that any positive ground state solutions with Morse index 1 or Morse index $N$ must be the form of $(d_{1}w,d_{2}w,\cdots,d_{N}w)$ under suitable conditions, where $w$ is the unique positive ground state solution of certain equation. Finally, we generalize our results to fractional $N$-coupled Schrödinger system.
Journal Article Details
Publisher Name: Global Science Press
Language: English
DOI: https://doi.org/10.4208/ata.2021.pr80.07
Analysis in Theory and Applications, Vol. 37 (2021), Iss. 2 : pp. 230–266
Published online: 2021-01
AMS Subject Headings: Global Science Press
Copyright: COPYRIGHT: © Global Science Press
Pages: 37
Keywords: Nonlinear Schrödinger system unique ground state solution variational method Morse indices.

