Year: 2021
Author: Tiexiang Li, Wen-Wei Lin, Yiqian Wang, Shing-Tung Yau
Analysis in Theory and Applications, Vol. 37 (2021), Iss. 4 : pp. 481–519
Abstract
In this paper, we propose a new method to study intermittent behaviors of coupled piecewise-expanding map lattices. We show that the successive transition between ordered and disordered phases occurs for almost every orbit when the coupling is small. That is,
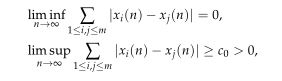
where $x_i(n)$ correspond to the coordinates of $m$ nodes at the iterative step $n$. Moreover, when the uncoupled system is generated by the tent map and the lattice consists of two nodes, we prove a phase transition occurs between synchronization and intermittent behaviors. That is, $$\lim_{n\rightarrow \infty}| x_1(n)-x_2(n)|=0\quad\text{for }\ \ \Big|c-\frac12\Big|<\frac14$$ and intermittent behaviors occur for $|c-\frac12|>\frac14$, where $0\le c\le 1$ is the coupling.
Journal Article Details
Publisher Name: Global Science Press
Language: English
DOI: https://doi.org/10.4208/ata.OA-2020-0020
Analysis in Theory and Applications, Vol. 37 (2021), Iss. 4 : pp. 481–519
Published online: 2021-01
AMS Subject Headings: Global Science Press
Copyright: COPYRIGHT: © Global Science Press
Pages: 39
Keywords: Synchronization pseudo synchronization phase transition Coupled map Lattices piecewise expanding map.