Close Search Advanced
Journals
Resources
About Us
Open Access

Fixed-Point Continuation Applied to Compressed Sensing: Implementation and Numerical Experiments

Fixed-Point Continuation Applied to Compressed Sensing: Implementation and Numerical Experiments
Preview
Add to basket

Year:    2010

Author:    Elaine T. Hale, Wotao Yin, Yin Zhang

Journal of Computational Mathematics, Vol. 28 (2010), Iss. 2 : pp. 170–194

Abstract

Fixed-point continuation (FPC) is an approach, based on operator-splitting and continuation, for solving minimization problems with $\ell_1$-regularization:

image.png


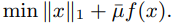
We investigate the application of this algorithm to compressed sensing signal recovery, in which $f(x) = \frac{1}{2}\|Ax-b\|_M^2$, $A \in \mathbb{R}^{m \times n}$ and $m \leq n$.  In particular, we extend the original algorithm to obtain better practical results, derive appropriate choices for $M$ and $\bar{\mu}$ under a given measurement model, and present numerical results for a variety of compressed sensing problems. The numerical results show that the performance of our algorithm compares favorably with that of several recently proposed algorithms.

Submit Article

You do not have full access to this article.

Already a Subscriber? Sign in as an individual or via your institution

Journal Article Details

Publisher Name:    Global Science Press

Language:    English

DOI:    https://doi.org/10.4208/jcm.2009.10-m1007

Journal of Computational Mathematics, Vol. 28 (2010), Iss. 2 : pp. 170–194

Published online:    2010-01

AMS Subject Headings:   

Copyright:    COPYRIGHT: © Global Science Press

Pages:    25

Keywords:    $\ell_1$ regularization Fixed-point algorithm Continuation Compressed sensing Numerical experiments.

Author Details

Elaine T. Hale

Wotao Yin

Yin Zhang

  1. The In-Crowd Algorithm for Fast Basis Pursuit Denoising

    Gill, Patrick R. | Wang, Albert | Molnar, Alyosha

    IEEE Transactions on Signal Processing, Vol. 59 (2011), Iss. 10 P.4595

    https://doi.org/10.1109/TSP.2011.2161292 [Citations: 117]

  2. Analog sparse approximation for compressed sensing recovery

    Rozell, Christopher J. | Garrigues, Pierre

    2010 Conference Record of the Forty Fourth Asilomar Conference on Signals, Systems and Computers, (2010), P.822

    https://doi.org/10.1109/ACSSC.2010.5757680 [Citations: 3]

  3. Multiresolution Parameter Choice Method for Total Variation Regularized Tomography

    Niinimäki, Kati | Lassas, Matti | Hämäläinen, Keijo | Kallonen, Aki | Kolehmainen, Ville | Niemi, Esa | Siltanen, Samuli

    SIAM Journal on Imaging Sciences, Vol. 9 (2016), Iss. 3 P.938

    https://doi.org/10.1137/15M1034076 [Citations: 15]

  4. Simultaneous reconstruction of undersampled multichannel signals with a decayed and time-delayed common component

    Shiraki, Yoshifumi | Kamamoto, Yutaka | Moriya, Takehiro

    2013 IEEE International Conference on Acoustics, Speech and Signal Processing, (2013), P.3816

    https://doi.org/10.1109/ICASSP.2013.6638372 [Citations: 0]

  5. Strong Convergence of Hybrid Algorithm for Asymptotically Nonexpansive Mappings in Hilbert Spaces

    Su, Juguo | Tang, Yuchao | Liu, Liwei | Chen, Rudong

    Journal of Applied Mathematics, Vol. 2012 (2012), Iss. 1

    https://doi.org/10.1155/2012/170540 [Citations: 0]

  6. Inexact accelerated augmented Lagrangian methods

    Kang, Myeongmin | Kang, Myungjoo | Jung, Miyoun

    Computational Optimization and Applications, Vol. 62 (2015), Iss. 2 P.373

    https://doi.org/10.1007/s10589-015-9742-8 [Citations: 26]

  7. Convergence Theorem of Hybrid Iterative Algorithm for Equilibrium Problems and Fixed Point Problems of Finite Families of Uniformly Asymptotically Nonexpansive Semigroups

    Liu, Hongbo | Li, Yi

    Advances in Pure Mathematics, Vol. 04 (2014), Iss. 06 P.244

    https://doi.org/10.4236/apm.2014.46033 [Citations: 0]
  8. Scale Space and Variational Methods in Computer Vision

    An Efficient Line Search for Sparse Reconstruction

    Shabani, Shima | Breuß, Michael

    2023

    https://doi.org/10.1007/978-3-031-31975-4_36 [Citations: 0]

  9. A mixed ℓ1 regularization approach for sparse simultaneous approximation of parameterized PDEs

    Dexter, Nick | Tran, Hoang | Webster, Clayton

    ESAIM: Mathematical Modelling and Numerical Analysis, Vol. 53 (2019), Iss. 6 P.2025

    https://doi.org/10.1051/m2an/2019048 [Citations: 8]

  10. Collaborative Multi-Sensor Classification Via Sparsity-Based Representation

    Dao, Minh | Nguyen, Nam H. | Nasrabadi, Nasser M. | Tran, Trac D.

    IEEE Transactions on Signal Processing, Vol. 64 (2016), Iss. 9 P.2400

    https://doi.org/10.1109/TSP.2016.2521605 [Citations: 21]

  11. Sample Approximation-Based Deflation Approaches for Chance SINR Constrained Joint Power and Admission Control

    Liu, Ya-Feng | Hong, Mingyi | Song, Enbin

    IEEE Transactions on Wireless Communications, Vol. (2016), Iss. P.1

    https://doi.org/10.1109/TWC.2016.2542240 [Citations: 12]

  12. A box constrained gradient projection algorithm for compressed sensing

    Broughton, R.L. | Coope, I.D. | Renaud, P.F. | Tappenden, R.E.H.

    Signal Processing, Vol. 91 (2011), Iss. 8 P.1985

    https://doi.org/10.1016/j.sigpro.2011.03.003 [Citations: 7]

  13. Sparse Approximation via Penalty Decomposition Methods

    Lu, Zhaosong | Zhang, Yong

    SIAM Journal on Optimization, Vol. 23 (2013), Iss. 4 P.2448

    https://doi.org/10.1137/100808071 [Citations: 131]

  14. A diagonally scaled Newton-type proximal method for minimization of the models with nonsmooth composite cost functions

    Aminifard, Zohre | Babaie–Kafaki, Saman

    Computational and Applied Mathematics, Vol. 42 (2023), Iss. 8

    https://doi.org/10.1007/s40314-023-02494-5 [Citations: 0]

  15. A smoothing SQP framework for a class of composite $$L_q$$ L q minimization over polyhedron

    Liu, Ya-Feng | Ma, Shiqian | Dai, Yu-Hong | Zhang, Shuzhong

    Mathematical Programming, Vol. 158 (2016), Iss. 1-2 P.467

    https://doi.org/10.1007/s10107-015-0939-5 [Citations: 29]

  16. Large sparse signal recovery by conjugate gradient algorithm based on smoothing technique

    Zhu, Hong | Xiao, Yunhai | Wu, Soon-Yi

    Computers & Mathematics with Applications, Vol. 66 (2013), Iss. 1 P.24

    https://doi.org/10.1016/j.camwa.2013.04.022 [Citations: 22]

  17. A new generalized shrinkage conjugate gradient method for sparse recovery

    Esmaeili, Hamid | Shabani, Shima | Kimiaei, Morteza

    Calcolo, Vol. 56 (2019), Iss. 1

    https://doi.org/10.1007/s10092-018-0296-x [Citations: 25]

  18. An approximate Newton-type proximal method using symmetric rank-one updating formula for minimizing the nonsmooth composite functions

    Aminifard, Zohre | Babaie-Kafaki, Saman

    Optimization Methods and Software, Vol. 38 (2023), Iss. 3 P.529

    https://doi.org/10.1080/10556788.2022.2142587 [Citations: 1]

  19. Modified conjugate gradient method for solving sparse recovery problem with nonconvex penalty

    Aminifard, Zohre | Hosseini, Alireza | Babaie-Kafaki, Saman

    Signal Processing, Vol. 193 (2022), Iss. P.108424

    https://doi.org/10.1016/j.sigpro.2021.108424 [Citations: 11]

  20. Time and Location Aware Mobile Data Pricing

    Ma, Qian | Liu, Ya-Feng | Huang, Jianwei

    IEEE Transactions on Mobile Computing, Vol. 15 (2016), Iss. 10 P.2599

    https://doi.org/10.1109/TMC.2015.2503763 [Citations: 29]

  21. A Barzilai-Borwein type method for minimizing composite functions

    Huang, Yakui | Liu, Hongwei

    Numerical Algorithms, Vol. 69 (2015), Iss. 4 P.819

    https://doi.org/10.1007/s11075-014-9927-8 [Citations: 11]

  22. Signal reconstruction by conjugate gradient algorithm based on smoothing $$l_1$$-norm

    Wu, Caiying | Zhan, Jiaming | Lu, Yue | Chen, Jein-Shan

    Calcolo, Vol. 56 (2019), Iss. 4

    https://doi.org/10.1007/s10092-019-0340-5 [Citations: 8]

  23. A new class of conjugate gradient methods for unconstrained smooth optimization and absolute value equations

    Rahpeymaii, Farzad | Amini, Keyvan | Allahviranloo, Tofigh | Malkhalifeh, Mohsen Rostamy

    Calcolo, Vol. 56 (2019), Iss. 1

    https://doi.org/10.1007/s10092-018-0298-8 [Citations: 5]

  24. Analysis and Generalizations of the Linearized Bregman Method

    Yin, Wotao

    SIAM Journal on Imaging Sciences, Vol. 3 (2010), Iss. 4 P.856

    https://doi.org/10.1137/090760350 [Citations: 127]

  25. Randomized Block Proximal Damped Newton Method for Composite Self-Concordant Minimization

    Lu, Zhaosong

    SIAM Journal on Optimization, Vol. 27 (2017), Iss. 3 P.1910

    https://doi.org/10.1137/16M1082767 [Citations: 4]

  26. A Fast Algorithm for Sparse Reconstruction Based on Shrinkage, Subspace Optimization, and Continuation

    Wen, Zaiwen | Yin, Wotao | Goldfarb, Donald | Zhang, Yin

    SIAM Journal on Scientific Computing, Vol. 32 (2010), Iss. 4 P.1832

    https://doi.org/10.1137/090747695 [Citations: 141]

  27. Iterative reweighted minimization methods for $$l_p$$ l p regularized unconstrained nonlinear programming

    Lu, Zhaosong

    Mathematical Programming, Vol. 147 (2014), Iss. 1-2 P.277

    https://doi.org/10.1007/s10107-013-0722-4 [Citations: 84]
  28. A Mathematical Introduction to Compressive Sensing

    Algorithms for ℓ1-Minimization

    Foucart, Simon | Rauhut, Holger

    2013

    https://doi.org/10.1007/978-0-8176-4948-7_15 [Citations: 0]

  29. Generalized Conjugate Gradient Methods for ℓ1 Regularized Convex Quadratic Programming with Finite Convergence

    Lu, Zhaosong | Chen, Xiaojun

    Mathematics of Operations Research, Vol. 43 (2018), Iss. 1 P.275

    https://doi.org/10.1287/moor.2017.0865 [Citations: 5]

  30. Accelerated Bregman Method for Linearly Constrained $$\ell _1$$ – $$\ell _2$$ Minimization

    Kang, Myeongmin | Yun, Sangwoon | Woo, Hyenkyun | Kang, Myungjoo

    Journal of Scientific Computing, Vol. 56 (2013), Iss. 3 P.515

    https://doi.org/10.1007/s10915-013-9686-z [Citations: 20]

  31. Alternating Direction Algorithms for $\ell_1$-Problems in Compressive Sensing

    Yang, Junfeng | Zhang, Yin

    SIAM Journal on Scientific Computing, Vol. 33 (2011), Iss. 1 P.250

    https://doi.org/10.1137/090777761 [Citations: 842]

  32. Combining line search and trust-region methods forℓ1-minimization

    Esmaeili, Hamid | Rostami, Majid | Kimiaei, Morteza

    International Journal of Computer Mathematics, Vol. 95 (2018), Iss. 10 P.1950

    https://doi.org/10.1080/00207160.2017.1346241 [Citations: 4]

  33. Golden Ratio Primal-Dual Algorithm with Linesearch

    Chang, Xiao-Kai | Yang, Junfeng | Zhang, Hongchao

    SIAM Journal on Optimization, Vol. 32 (2022), Iss. 3 P.1584

    https://doi.org/10.1137/21M1420319 [Citations: 9]

  34. Nonmonotone variable metric Barzilai-Borwein method for composite minimization problem

    Guo, Xiao | Xu, Chuanpei | Zhu, Zhibin | Zhang, Benxin

    AIMS Mathematics, Vol. 9 (2024), Iss. 6 P.16335

    https://doi.org/10.3934/math.2024791 [Citations: 0]

  35. Sparse microwave imaging: Principles and applications

    Zhang, BingChen | Hong, Wen | Wu, YiRong

    Science China Information Sciences, Vol. 55 (2012), Iss. 8 P.1722

    https://doi.org/10.1007/s11432-012-4633-4 [Citations: 132]

  36. Accelerated iterative hard thresholding algorithm for $$l_0$$ regularized regression problem

    Wu, Fan | Bian, Wei

    Journal of Global Optimization, Vol. 76 (2020), Iss. 4 P.819

    https://doi.org/10.1007/s10898-019-00826-6 [Citations: 7]

  37. Strong Convergence by a Hybrid Algorithm for Finding a Common Fixed Point of Lipschitz Pseudocontraction and Strict Pseudocontraction in Hilbert Spaces

    Ungchittrakool, Kasamsuk | Wong, P. J. Y.

    Abstract and Applied Analysis, Vol. 2011 (2011), Iss. 1

    https://doi.org/10.1155/2011/530683 [Citations: 2]

  38. Iteratively reweighted sparse reconstruction in impulsive noise

    He, Zhen-Qing | Shi, Zhi-Ping | Huang, Lei | So, H. C.

    2015 IEEE China Summit and International Conference on Signal and Information Processing (ChinaSIP), (2015), P.741

    https://doi.org/10.1109/ChinaSIP.2015.7230503 [Citations: 1]

  39. Strong convergence theorem for pseudo-contractive mappings in Hilbert spaces

    Tang, Yu-Chao | Peng, Ji-Gen | Liu, Li-Wei

    Nonlinear Analysis: Theory, Methods & Applications, Vol. 74 (2011), Iss. 2 P.380

    https://doi.org/10.1016/j.na.2010.08.048 [Citations: 16]

  40. SCIHTBB: Sparsity constrained iterative hard thresholding with Barzilai–Borwein step size

    Xie, Zhipeng | Chen, Songcan

    Neurocomputing, Vol. 74 (2011), Iss. 17 P.3663

    https://doi.org/10.1016/j.neucom.2011.07.003 [Citations: 3]

  41. An iteratively approximated gradient projection algorithm for sparse signal reconstruction

    Liu, Zhongyi | Wei, Zhihui | Sun, Wenyu

    Applied Mathematics and Computation, Vol. 228 (2014), Iss. P.454

    https://doi.org/10.1016/j.amc.2013.10.063 [Citations: 5]

  42. Proximity point algorithm for low-rank matrix recovery from sparse noise corrupted data

    Zhu, Wei | Shu, Shi | Cheng, Li-zhi

    Applied Mathematics and Mechanics, Vol. 35 (2014), Iss. 2 P.259

    https://doi.org/10.1007/s10483-014-1788-6 [Citations: 4]

  43. Hybrid method for equilibrium problems and fixed point problems of finite families of nonexpansive semigroups

    Eslamian, Mohammad

    Revista de la Real Academia de Ciencias Exactas, Fisicas y Naturales. Serie A. Matematicas, Vol. 107 (2013), Iss. 2 P.299

    https://doi.org/10.1007/s13398-012-0069-3 [Citations: 13]

  44. An Exp Model with Spatially Adaptive Regularization Parameters for Multiplicative Noise Removal

    Na, Hanwool | Kang, Myeongmin | Jung, Miyoun | Kang, Myungjoo

    Journal of Scientific Computing, Vol. 75 (2018), Iss. 1 P.478

    https://doi.org/10.1007/s10915-017-0550-4 [Citations: 6]

  45. A Barzilai–Borwein-Like Iterative Half Thresholding Algorithm for the $$L_{1/2}$$ L 1 / 2 Regularized Problem

    Wu, Lei | Sun, Zhe | Li, Dong-Hui

    Journal of Scientific Computing, Vol. 67 (2016), Iss. 2 P.581

    https://doi.org/10.1007/s10915-015-0094-4 [Citations: 8]