The Numerical Stability of the $\theta$-Method for Delay Differential Equations with Many Variable Delays
Year: 1999
Author: Lin Qiu, Taketomo Mitsui, Jiao-Xun Kuang
Journal of Computational Mathematics, Vol. 17 (1999), Iss. 5 : pp. 523–532
Abstract
This paper deals with the asymptotic stability of theoretical solutions and numerical methods for the delay differential equations (DDEs)
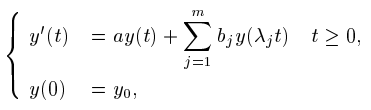
where $a, b_1, b_2, ... b_m$ and $y_0 \in C, 0 < \lambda_m \le \lambda_{m-1} \le ... \le \lambda_1<1$. A sufficient condition such that the differential equations are asymptotically stable is derived. And it is shown that the linear $\theta$-method is $\bigwedge GP_m$-stable if and only if $\frac{1}{2} \le \theta \le 1$.
You do not have full access to this article.
Already a Subscriber? Sign in as an individual or via your institution
Journal Article Details
Publisher Name: Global Science Press
Language: English
DOI: https://doi.org/1999-JCM-9122
Journal of Computational Mathematics, Vol. 17 (1999), Iss. 5 : pp. 523–532
Published online: 1999-01
AMS Subject Headings:
Copyright: COPYRIGHT: © Global Science Press
Pages: 10
Keywords: Delay differential equation Variable delays Numerical stability $\theta$-methods.