Oscillation Theory of h-Fractional Difference Equations
Year: 2021
Author: Fanfan Li, Zhenlai Han
Journal of Nonlinear Modeling and Analysis, Vol. 3 (2021), Iss. 1 : pp. 105–113
Abstract
In this paper, we initiate the oscillation theory for h-fractional
difference equations of the form
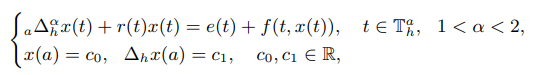
where a∆αh is the Riemann-Liouville h-fractional difference of order α, Tah:={a+kh,k∈Z+∪{0}}, and a≥0, h>0. We study the oscillation of h-fractional difference equations with Riemann-Liouville derivative, and obtain
some sufficient conditions for oscillation of every solution. Finally, we give an
example to illustrate our main results.
You do not have full access to this article.
Already a Subscriber? Sign in as an individual or via your institution
Journal Article Details
Publisher Name: Global Science Press
Language: English
DOI: https://doi.org/10.12150/jnma.2021.105
Journal of Nonlinear Modeling and Analysis, Vol. 3 (2021), Iss. 1 : pp. 105–113
Published online: 2021-01
AMS Subject Headings:
Copyright: COPYRIGHT: © Global Science Press
Pages: 9
Keywords: h-deference equations Oscillation Fractional.
Author Details
Fanfan Li Email
Zhenlai Han Email

