The Existence and Multiplicity of Normalized Solutions for Kirchhoff Equations in Defocusing Case
Year: 2024
Author: Lin Xu
Analysis in Theory and Applications, Vol. 40 (2024), Iss. 2 : pp. 191–207
Abstract
In this paper, we study the existence of solutions for Kirchhoff equation
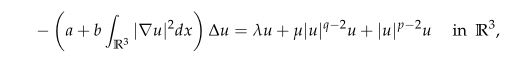
with mass constraint condition
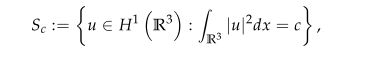
where a, b, c>0, μ∈R and 2<q<p<6. The λ∈R appears as a Lagrange multiplier. For the range of p and q, the Sobolev critical exponent 6 and mass critical exponent 143 are involved which corresponding energy functional is unbounded from below on Sc. We consider the defocusing case, i.e. μ<0 when (p,q) belongs to a certain domain in R2. We prove the existence and multiplicity of normalized solutions by using constraint minimization, concentration compactness principle and Minimax methods. We partially extend the results that have been studied.
You do not have full access to this article.
Already a Subscriber? Sign in as an individual or via your institution
Journal Article Details
Publisher Name: Global Science Press
Language: English
DOI: https://doi.org/10.4208/ata.OA-2023-0027
Analysis in Theory and Applications, Vol. 40 (2024), Iss. 2 : pp. 191–207
Published online: 2024-01
AMS Subject Headings: Global Science Press
Copyright: COPYRIGHT: © Global Science Press
Pages: 17
Keywords: Normalized solutions Kirchhoff-type equation mixed nonlinearity.
Author Details
Lin Xu Email

