Year: 2022
Author: Ruggero Freddi
Analysis in Theory and Applications, Vol. 38 (2022), Iss. 1 : pp. 26–78
Abstract
In this paper we consider the Dirichlet problem
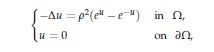
where $\rho$ is a small parameter and $\Omega$ is a $C^2$ bounded domain in $\mathbb{R}^2$. In [1], the author proves the existence of a $m$-point blow-up solution $u_\rho$ jointly with its asymptotic behaviour. We compute the Morse index of $u_\rho$ in terms of the Morse index of the associated Hamilton function of this problem. In addition, we give an asymptotic estimate for the first $4m$ eigenvalues and eigenfunctions.
You do not have full access to this article.
Already a Subscriber? Sign in as an individual or via your institution
Journal Article Details
Publisher Name: Global Science Press
Language: English
DOI: https://doi.org/10.4208/ata.OA-2020-0037
Analysis in Theory and Applications, Vol. 38 (2022), Iss. 1 : pp. 26–78
Published online: 2022-01
AMS Subject Headings: Global Science Press
Copyright: COPYRIGHT: © Global Science Press
Pages: 53
Keywords: Morse index sinh-Poisson equation eigenvalues estimates.

