Year: 2021
Author: Jiaquan Liu, Xiangqing Liu, Zhi-Qiang Wang
Analysis in Theory and Applications, Vol. 37 (2021), Iss. 2 : pp. 209–229
Abstract
The existence of an infinite sequence of sign-changing solutions are proved for a class of quasilinear elliptic equations under suitable conditions on the quasilinear coefficients and the nonlinearity
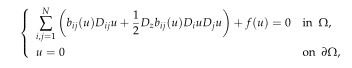
where $\Omega\subset\mathbb{R}^N$ is a bounded domain with smooth boundary, and we use
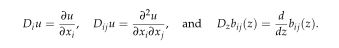
The main interest of this paper is for the case of bounded quasilinearity $b_{ij}$. The result is proved by an elliptic regularization method involving truncations of both $u$ and the gradient of $u$.
Journal Article Details
Publisher Name: Global Science Press
Language: English
DOI: https://doi.org/10.4208/ata.2021.pr80.02
Analysis in Theory and Applications, Vol. 37 (2021), Iss. 2 : pp. 209–229
Published online: 2021-01
AMS Subject Headings: Global Science Press
Copyright: COPYRIGHT: © Global Science Press
Pages: 21
Keywords: Quasilinear elliptic equations sign-changing solution an elliptic regularization method.

